Comment les scientifiques ont-ils « pesé » la Terre ?

Charles de Izarra, INSA Centre Val de Loire

Cet article est publié dans le cadre de la Fête de la science, qui a lieu du 1^er au 11 octobre 2021 en métropole et du 5 au 22 novembre 2021 en outre-mer et à l’international, et dont The Conversation France est partenaire. Cette édition a pour thème : « Eureka ! L’émotion de la découverte ». Retrouvez tous les événements de votre région sur le site Fetedelascience.fr.

Nous naissons, nous vivons, nous nous aimons et nous mourrons sur cette planète Terre, que l’on assimile à une boule. C’est notre vaisseau spatial depuis toujours et il se déplace autour du Soleil à la vitesse cosmique de 30 km par seconde sur une orbite elliptique.

Dans les encyclopédies, on trouve toutes sortes d’informations sur cette Terre, et notamment combien elle pèse… Mais comment donc cette masse a-t-elle bien pu être déterminée ? Sa mesure fait appel à quelques lois de la mécanique classique, branche fondamentale de la physique, et à un ingénieux dispositif expérimental utilisé par le savant anglais Henry Cavendish il y a un peu plus de deux cents ans.

Tentons d’expliquer avec une terminologie du XXI^e siècle comment une telle mesure a été possible…

La loi de la gravitation universelle

Avant toute chose, il faut comprendre que la masse de la Terre n’est pas déterminée de manière directe : elle est déduite de la mesure d’autres grandeurs que nous allons explorer par la suite.

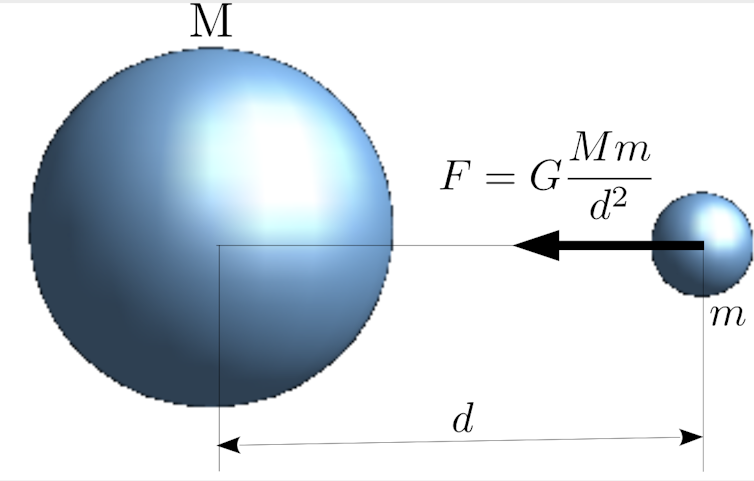
Le point de départ est celui de la loi de la gravitation universelle, proposée et validée par Isaac Newton sur la base de données astronomiques : elle fournit la force d’interaction F essentiellement attractive entre deux masses M et m séparées par une distance d. La force de gravitation est proportionnelle au produit de ces deux masses, et inversement proportionnelle au carré de la distance séparant ces deux masses.

Comme dans toute formule physique, il convient d’introduire une constante pour tenir compte des systèmes d’unités utilisés (masses en kilogrammes, longueurs en mètres et forces en newtons). Cette constante est appelée « constante de Newton » ou « constance de gravitation ». Elle est notée G et fait partie des constantes fondamentales de la physique.

Sur Terre, G se cache dans g et la force de gravitation devient ce qu’on appelle le poids…

La formule pour peser la Terre

Revenons maintenant sur Terre avec les hypothèses simplificatrices suivantes : la Terre est une boule de rayon R_T, de masse totale M_T répartie sous forme de couches sphériques de densités différentes.

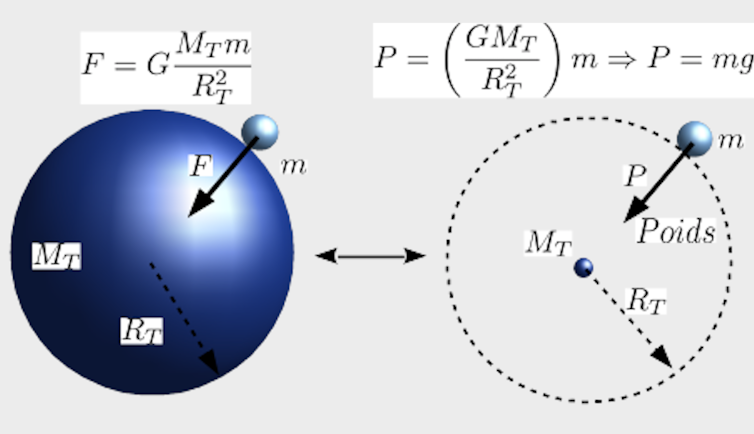
La loi de la gravitation universelle calculée avec une masse m à la surface de la Terre est obtenue de la manière suivante : on réduit la Terre à une masse ponctuelle localisée en son centre, et la masse m située sur la surface terrestre est placée à la distance R_T de la masse ponctuelle M_T.

On ne laisse pas ici la loi de la gravitation sous sa forme générique ; tout d’abord, on change la dénomination de cette force qui devient le poids (nous le noterons P), et l’on groupe tout naturellement le produit GM_T/R_T² pour fabriquer l’accélération de la pesanteur g donnée en m/s².

À partir des formules présentées ci-dessus, on remarque que si l’accélération de la pesanteur g, le rayon de la Terre R_T et la constante de gravitation G sont connus, alors on peut en déduire la masse de la Terre : M_T = gR_T²/G reste à faire les mesures !

Le rayon de la Terre

Je n’insisterai pas sur la mesure du rayon de la Terre qui pourrait à elle seule faire l’objet d’un autre article : sa valeur est d’environ de 6400 km. Soulignons toutefois qu’il est facile de réitérer sa mesure faite par le philosophe grec Eratosthène (vers l’an 230 av. J.-C.) avec les moyens modernes dont nous disposons (GPS, téléphones mobiles pour la simultanéité des mesures…). Cette expérience a d’ailleurs été proposée à des élèves de collèges et de lycées.

L’accélération de la pesanteur

L’accélération de la pesanteur g correspond à l’accélération que subit un objet soumis à l’attraction de la Terre. Lorsque l’on tombe d’une échelle, on débute avec une vitesse nulle, mais celle-ci est rapidement augmentée pour heurter le sol. La variation de cette vitesse est mesurée avec l’accélération de la pesanteur qui peut être déterminée avec une expérience de chute libre ou mieux encore, avec un oscillateur mécanique qui repasse dans les mêmes conditions de manière périodique et qui est donc beaucoup plus adapté à la mesure.

On sait depuis les travaux des scientifiques Christian Huygens et de Robert Hooke, au 17^e siècle, que la période d’un pendule simple – c’est-à-dire la durée de son aller-retour autour de la position repos – fabriqué avec une masse ponctuelle fixée à l’extrémité d’une tige rigide, fait intervenir le poids, donc l’accélération de la pesanteur g.

Une mesure de la période d’oscillation d’un pendule permet de déterminer la valeur de l’accélération de la pesanteur, qui est de 9,81 m/s². Je passe sous silence les différentes subtilités expérimentales concernant l’étude des pendules, ainsi que les variations de l’accélération de la pesanteur en fonction de la latitude – effet de la rotation de la Terre.

La constante de gravitation

C’est à cette étape que se trouve la clé de la mesure, mais aussi toute sa difficulté. En effet, on a vu que les forces gravitationnelles mises en jeu pour des masses de quelques kilogrammes, voire quelques centaines de kilogrammes, étaient extrêmement faibles, donc très difficiles à mesurer.

Le travail expérimental conduisant à déterminer la constante de gravitation est l’œuvre de Henry Cavendish et fait appel à un oscillateur mécanique de très grande sensibilité. Ses travaux originaux sur le sujet datent de 1798, et étaient principalement consacrés à la mesure de la densité moyenne de la Terre. Par la suite, sa balance a tout simplement été baptisée « balance à peser la Terre ».

La balance de Cavendish

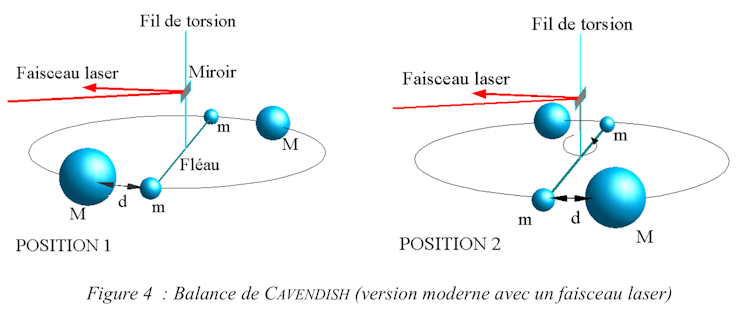
La balance de Cavendish est constituée d’un fléau (une tige) horizontal aux extrémités duquel sont fixées deux petites masses m (de l’ordre de 15 grammes).

Le fléau est suspendu à un fil de torsion vertical ; dans la plupart des balances modernes vendues par des sociétés spécialisées dans le matériel de travaux pratiques de physique, ce fil de torsion est un ruban de bronze très fin. Un miroir très léger lui est fixé : il permet, en utilisant un faisceau laser de faible puissance, de visualiser l’angle de rotation que fait le fléau autour de l’axe constitué par le fil de torsion : c’est la méthode de Poggendorff.

Deux masses M en plomb, de la taille d’une boule de pétanque, sont placées à une distance d de chaque masse m dans une position telle que le fléau se stabilise sous l’effet des forces de gravitation entre les masses M et m.

En faisant basculer les deux masses depuis la position 1 vers la position 2 symétrique, on provoque une rupture de l’équilibre des masses. Le fléau se met alors à osciller avec une période que l’on mesure pour déterminer la constante de torsion du fil, et se stabilise de nouveau autour d’une nouvelle position d’équilibre correspondant à la position 2. L’angle de rotation du pendule est suivi en mesurant la position du spot laser projeté sur un écran sur lequel est placée une échelle graduée.

L’écart entre les deux positions d’équilibre, mesuré à partir des deux positions du spot laser sur l’échelle graduée, donne les forces d’interactions gravitationnelles entre les masses.

Enfin, connaissant les valeurs des masses et des distances, on peut calculer la valeur de G en utilisant la loi de la gravitation universelle.

Sachant que la valeur de G est t : G = 6,67x10^-11 Nm2kg^-2, l’ordre de grandeur des forces à mesurer pour des masses de l’ordre du kilogramme distantes de 1 cm est de 7x10^-7 N.

Cette force correspond au poids d’une masse de 7x10^-8 kg, soit 7 centièmes de milligramme ; la balance de Cavendish est assez sensible pour détecter ce type de force, mais il convient d’éviter la présence de toute charge électrique dont les interactions sont très supérieures aux interactions entre masses et peuvent totalement masquer le phénomène gravitationnel.

Les puissances de dix et l’imagination

Connaissant maintenant G, R_T, et M_T, on peut calculer la masse de la Terre.

On obtient alors 6,10²⁴ kg. Est-ce une masse importante à l’échelle humaine ? Pour répondre, car il est très difficile de se figurer mentalement les puissances de dix, imaginons un dispositif permettant de prélever chaque seconde une masse de 1000 tonnes à une masse égale à 6,10²⁴ kg.

Pour épuiser la masse proposée (et j’invite la lectrice et le lecteur à vérifier ce résultat), il faut une durée égale à 190 milliards d’années. Cette durée est à comparer avec les 5 milliards d’années de l’âge du système solaire. Je laisse la lectrice ou le lecteur conclure…

Charles de Izarra, Chercheur, INSA Centre Val de Loire

Cet article est republié à partir de The Conversation sous licence Creative Commons. Lire l’article original.

Crédit visuel principal de Une : Nous devons cet exploit à Henry Cavendish et sa balance à peser la terre. Shutterstock